در بی نظمی، نظمی نهفته… به صدای زنگوله ها گوش کن!

مفهوم تفاوت: مبنایی برای درک و تحلیل

در جهان انسانی، ما مفاهیمی مانند خوب و بد، زشت و زیبا، و درست و غلط را ایجاد کرده‌ایم. با این حال، حقیقت این است که آنچه ما به‌عنوان انسان انجام می‌دهیم، تشخیص و تحلیل میزان تفاوت‌ها است. درک این تفاوت‌ها نه تنها به ما در زندگی روزمره کمک می‌کند، بلکه در حوزه هوش مصنوعی نیز به طراحی الگوریتم‌های پیشرفته منجر می‌شود. اما چگونه می‌توانیم میزان تفاوت‌ها را اندازه‌گیری و از آن‌ها استفاده کنیم؟

در دنیای هوش مصنوعی، پاسخ به این سوال، ما را قادر می‌سازد الگوریتم‌هایی بسازیم که بتوانند به داده‌های حساسیت‌زا واکنش مناسب نشان دهند و به‌طور مؤثر با داده‌ها تعامل داشته باشند. پس بیایید ببینیم چگونه می‌توان چنین تابعی را کشف کرد.

نقش آمار و احتمال در توضیح وقایع تصادفی

جهان ما در نگاه اول از متغیرهای تصادفی و بی‌نظم ساخته شده است که گاهی معنی خاصی ندارند. اما آیا در پس این بی‌نظمی ظاهری، نوعی نظم وجود دارد؟ برای بررسی این موضوع، بیایید یک رخداد تصادفی را بررسی کنیم.

فرض کنید دو تاس در اختیار داریم. هر بار که این دو تاس را پرتاب می‌کنیم، مجموع اعداد روی آن‌ها را یادداشت می‌کنیم. این عمل را ۱۰ بار تکرار می‌کنیم و نتایج زیر به دست می‌آید:

6، 10، 7، 5، 9، 9، 7، 6، 3، 10

اگر دقت کنید، متوجه می‌شوید که برخی از مجموع‌ها بیشتر از بقیه ظاهر می‌شوند. بنابراین، در مرحله بعد، شیوه یادداشت‌برداری خود را تغییر می‌دهیم و به‌جای یادداشت هر بار، تعداد دفعات تکرار هر مجموع را ثبت می‌کنیم. در جدول زیر نتایج حاصل از ۵۰ پرتاب تاس را مشاهده می‌کنید:

2: 2
3: 3
4: 7
5: 8
6: 5
7: 7
8: 6
9: 5
10: 4
11: 1
12: 2

این جدول به وضوح نشان می‌دهد که برخی اعداد، به‌ویژه اعداد میانی مانند ۵ تا ۸، بیشتر از اعداد ۲ یا ۱۲ تکرار می‌شوند. اما چرا این اتفاق می‌افتد؟

همیشه معلم‌ها گفتند که حالات مطلوب به روی کل حالت‌ها…

حالا به جای اینکه با آزمایش به شهود برسیم می‌خواهیم کمی دست به قلم بشویم و ببینیم چرا چنین اتفاقی رخ می‌دهد و انگار که داخل یکسری رخداد کاملا تصادفی و بی ربط داریم نظمی را پیدا می‌کنیم !

برای فهم این موضوع، باید به شمارش حالت‌های ممکن بپردازیم. جدول زیر نشان می‌دهد که هر مجموع چگونه به دست می‌آید:

2: 1+1
3: 1+2, 2+1
4: 1+3, 2+2, 3+1
5: 1+4, 2+3, 3+2, 4+1
6: 1+5, 2+4, 3+3, 4+2, 5+1
7: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1
8: 2+6, 3+5, 4+4, 5+3, 6+2
9: 3+6, 4+5, 5+4, 6+3
10: 4+6, 5+5, 6+4
11: 5+6, 6+5
12: 6+6

خب حالا ما لیست تمامی حالاتی که می‌توانند یک جمع خاص را بسازند داریم و کل حالات ما هم ۳۶ حالت است و با بررسی این حالت‌ها متوجه می‌شویم که اعداد میانی به دلیل تعداد بیشتر حالات ممکن، احتمال وقوع بیشتری دارند.

بصری سازی و تفکر عمیق

برای درک بهتر این موضوع، می‌توان از برنامه‌نویسی برای شبیه‌سازی و بصری‌سازی استفاده کرد. با کمک زبان پایتون و کتابخانه‌های Matplotlib و NumPy، می‌توان این پرتاب‌های تاس را شبیه‌سازی و نتایج را تحلیل کرد. برای شبیه‌سازی ۲۰ تاس و مشاهده توزیع نتایج، می‌توانید به کد مربوطه در لینک گیت‌هاب انتهای مقاله مراجعه کنید.

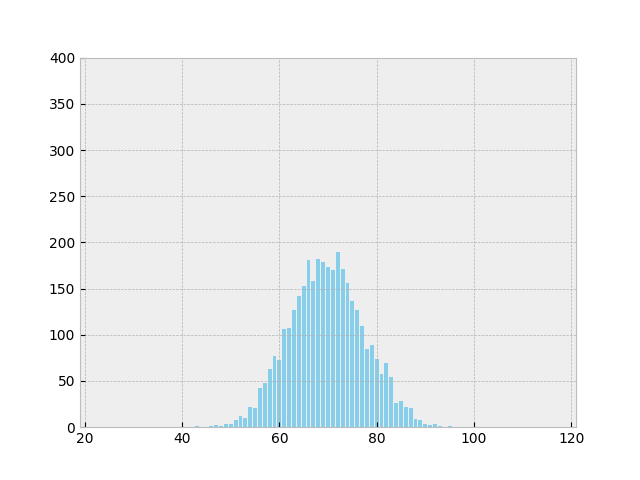
این تحلیل‌ها ما را به نمودار معروف زنگوله‌ای یا توزیع نرمال می‌رساند که یکی از مهم‌ترین مفاهیم در آمار و ریاضیات است.

این نمودار مفاهیم عمیق و زیادی از علم آمار را نمایش می‌دهد که وقتش هست معیار معروف دیگری در آمار را هم معرفی کنیم که دقیقا کارش تشخیص میزان پراکندگی حول میانگین داده هاست و نشان میدهد اکثریت داده ها در چه بازه ای از میانگین میچرخد. در تصویر زیر ما در نمودار زنگوله‌ای خودمان انحراف معیار مثبت و منفی را به نمایش گذاشته ایم:

دورنگاهی به کاربرد های عظیم نمودار توزیع نرمال در هوش مصنوعی و یادگیری ماشین

توزیع نرمال نه تنها پایه‌ای برای مفاهیم پیچیده‌تر مانند تابع سیگموید است، بلکه در الگوریتم‌های یادگیری ماشین نقش کلیدی دارد. به عنوان مثال، الگوریتم‌های بلور کردن تصاویر که در گوشی‌ها و کامپیوترها به‌کار می‌روند، بر اساس توزیع نرمال عمل می‌کنند.

همچنین، در پردازش تصویر و تشخیص اشیا، توزیع نرمال به کمک الگوریتم‌ها می‌آید تا مرزهای یک شیء را از پس‌زمینه جدا کند. به‌طور کلی، در تحلیل داده‌ها، توزیع نرمال به‌عنوان ابزاری کلیدی برای بررسی پراکندگی و تحلیل دقیق‌تر داده‌ها به‌کار می‌رود.

یکی از کاربرد های همیشگی که شما از این تابع ممکن است داشته باشید، الگوریتم‌های بلورسازی است که با گوشی یا کامپیوتر خود انجام می‌دهید و معمولا این نوع بلور کردن تصویر با اسم ‌Grassier blur شناخته می‌شود.

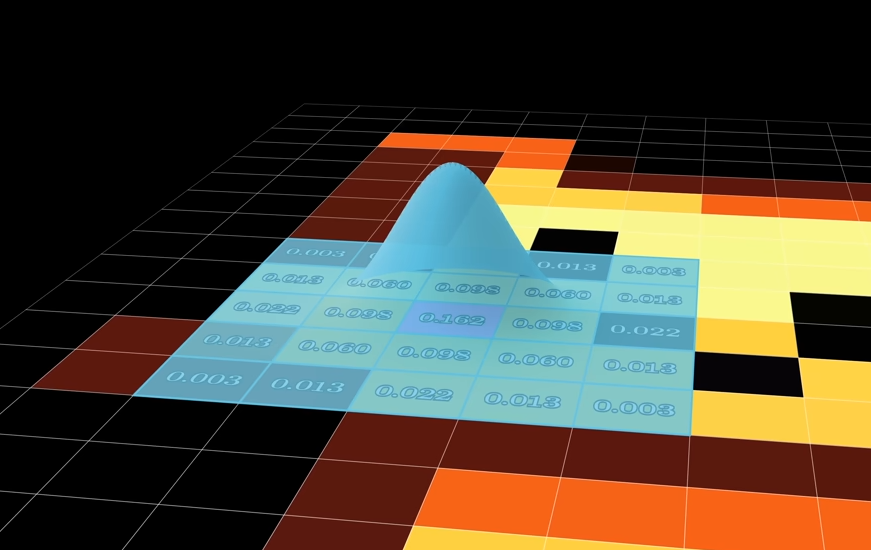
اما داستان برای همین بلور کردن عکس ها جایی جالب می‌شود که کاربرد آن را در الگوریتم های یادگیری ماشین پیشرفته برای تشخیص عکس و جدا کردن گوشه های یک شی از پشت صحنه استفاده می‌کنیم!

از انجایی که کار اصلی ما در یادگیری ماشین و هوش مصنوعی کار با داده ها است تابع توزیع نرمال به ما کمک بسیار زیادی در تمیز کردن و آنالیز این داده ها می‌کند.

لینک گیت‌لب کد های این مقاله:
https://gitlab.com/parsaishash/fun-math/-/tree/main/tas